三维空间中欧拉角的转动,当比较复杂的时候很难一次性想清楚。如何确定Kirchhoff杆正确的边界条件呢?下面给出一种直接求解的方法
确定杆两端在全局和局部标架中的表达
假设全局标架表达为
我们只需要通过
四元数直接求解
四元数的转动矩阵为:
通过
首先得到:
其次可以反解得到:
通过欧拉角求解
首先通过转动矩阵反解欧拉角 (mathematica函数EulerAngle),然后利用四元数与欧拉角的关系确定边界条件。四元数与欧拉角关系为:
Note: 这里有一点值得特别注意。之前通过四元数的变换为:
这里标架矢量均为行矢量,但是我们一般定义转动矩阵如下:
这里
转置后为:
由于单位矩阵是对称的,因此有:
从Eq. (8) 和 Eq. (11) 可以看出:
这一点在利用mathematica求解欧拉角的过程中需要特别注意。
符号计算程序
四元数直接求解:
1 | Clear["`*"] |
欧拉角间接求解:
1 | Clear["`*"] |
下面我们编写符号计算程序实现上面两种求解边界条件的方式,并通过案例进行验证。
IJSS 248 (2022) 111685
两端局部标架分别为:
可以解的与原文一致的边界条件:
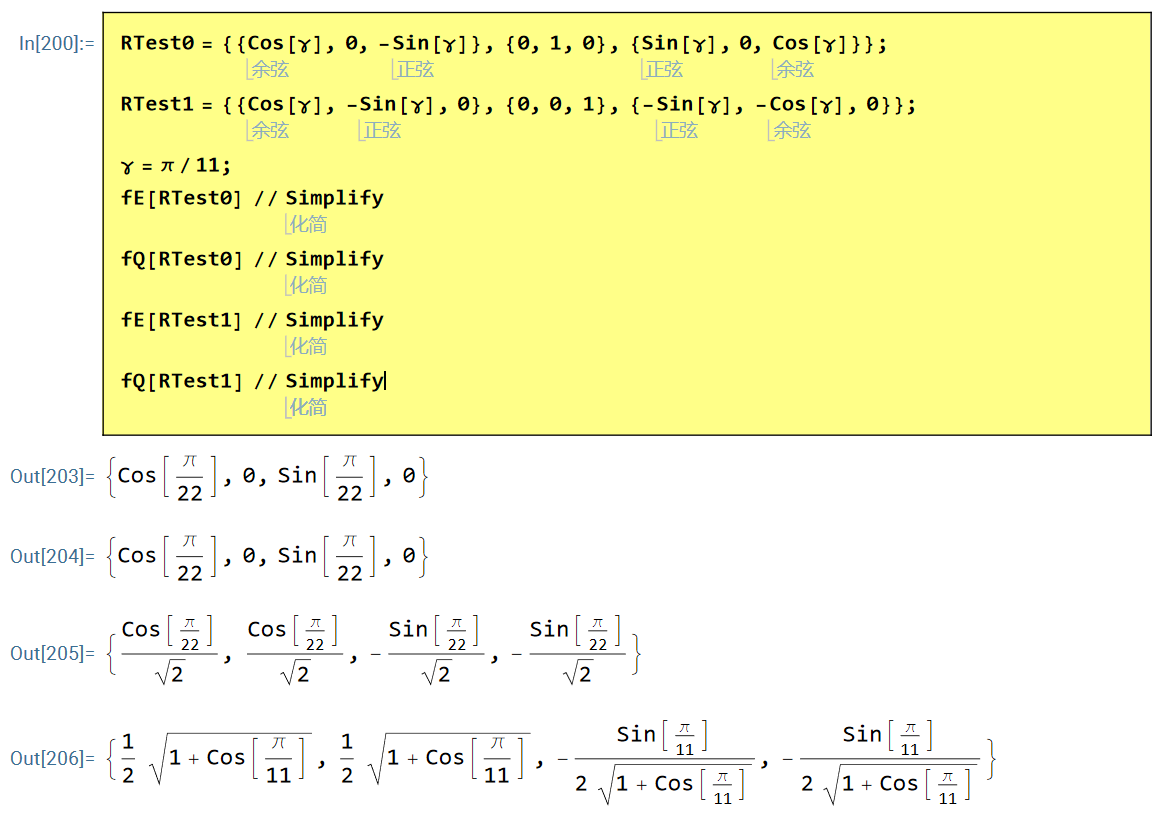

JMPS 122 (2019) 657–685
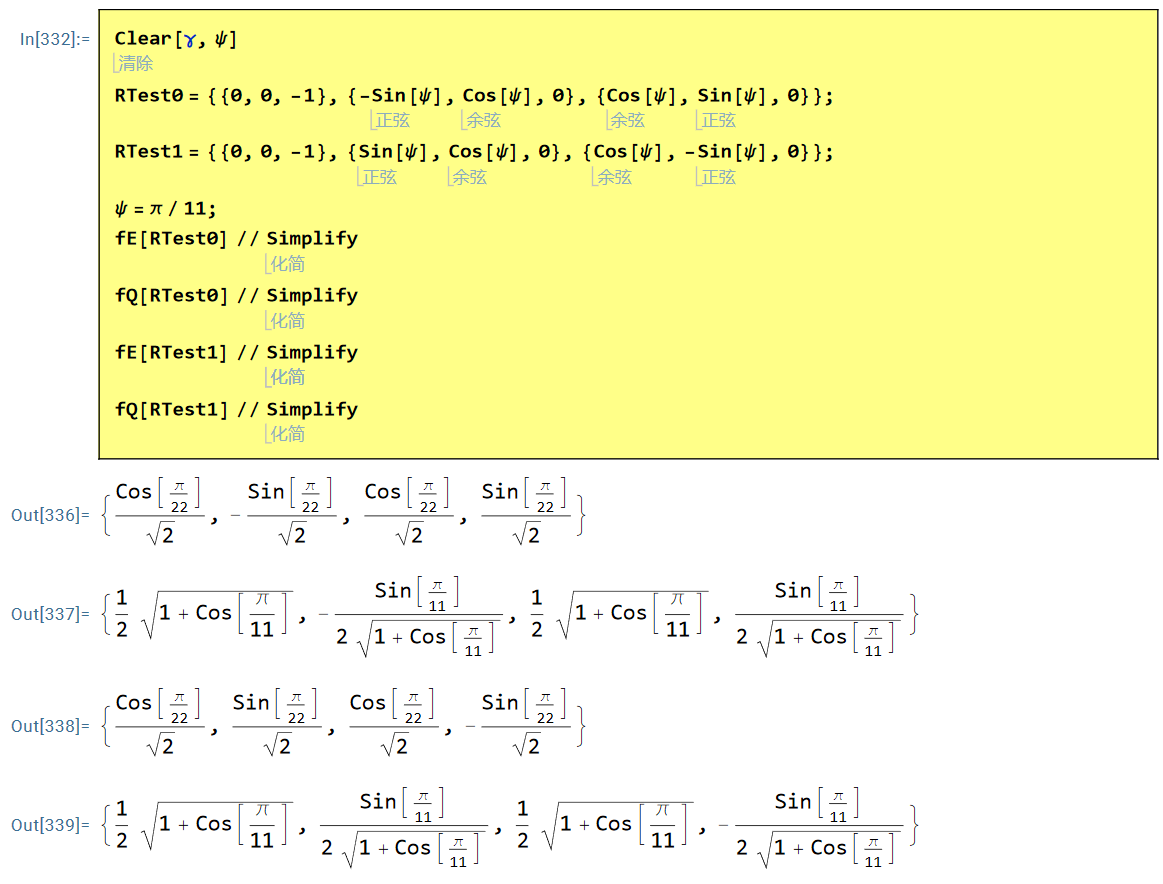
两端局部标架分别为:
可以解的与原文一致的边界条件:

作者: 得意喵~

