曲线浸入曲面(边界驱动生长)
概述
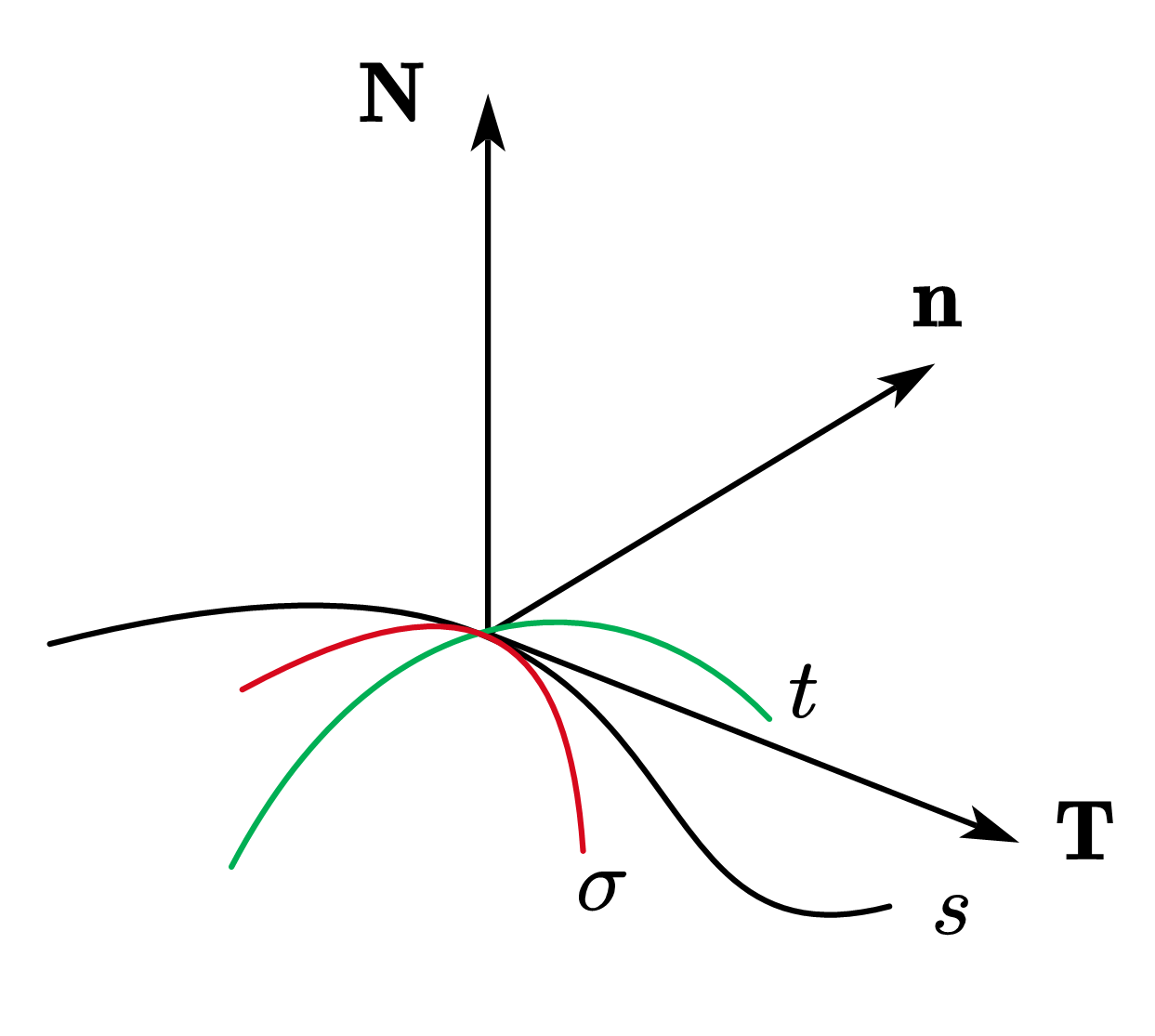
我们从生长模型的角度看这个问题,对于沿
定义曲面的度规:
度规的导数
曲线标架的变换关系
s方向
t方向
首先推导偏导数的对易关系:
曲面本构条件
首先得到第一第二基本型系数为:
由(8) ~ (11)计算得到Christoffel曲面的符号为:
Codazzi-Mainardi 方程
带入Mainardi方程得到:
化简得到:
Gauss-Bonnet 定理
本文采用CC-BY-SA-3.0协议,转载请注明出处
作者: 得意喵~
作者: 得意喵~

曲线浸入曲面(边界驱动生长)

我们从生长模型的角度看这个问题,对于沿
定义曲面的度规:
首先推导偏导数的对易关系:
首先得到第一第二基本型系数为:
由(8) ~ (11)计算得到Christoffel曲面的符号为:
带入Mainardi方程得到:
化简得到: