如何对具有周期性的模型进行旋转？

几何关系

假设左图是材料的最小周期型单元，经过旋转后得到右图的模型。要想满足周期性边界条件，假设方向上有个周期，方向上有个周期。需满足如下关系式：



得到：

同时需要满足体积守恒

最终解得：

只有时成立，也就是说除了转动180度的倍数，不存在旋转后仍未周期性的体系，晶格常数必然发生失配。
既然晶格常数无法满足旋转的要求，要想让容差率达到最小，应该如何做？

数值近似解

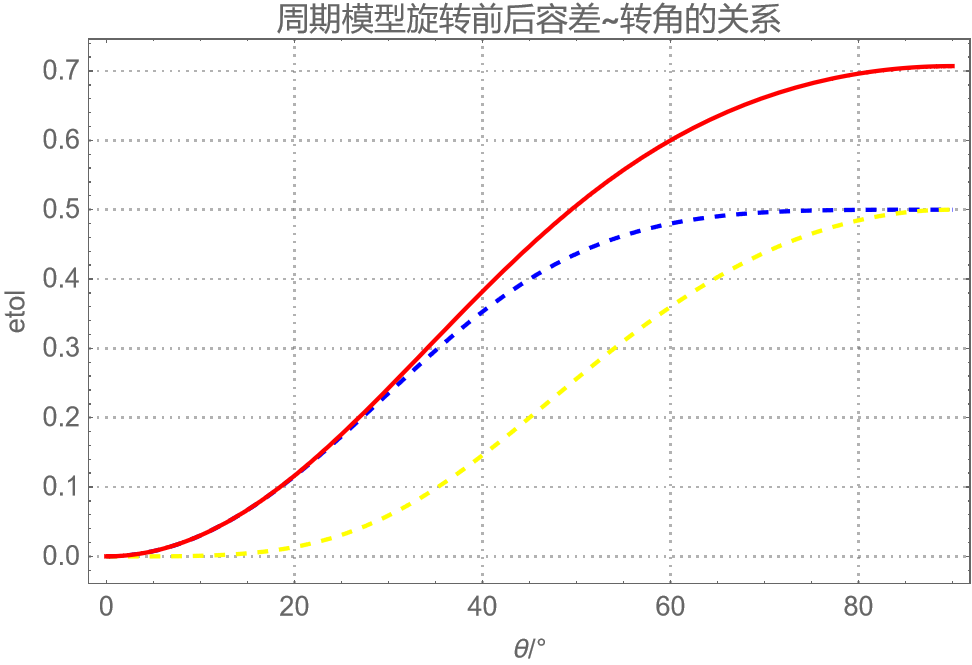
假设初始晶格比，蓝线为旋转后的体积容差，黄线为旋转后的横向键长容差，红线为总容差。

我们修改(1)式，引入容差来描述体积的变化率，来描述横向键长的变化（在0附近，在1附近）：

定义误差函数，最终求得误差以及晶格比与角度的变化。


误差函数的极小值可以解析求解为：





旋转前后的最佳晶格比为：

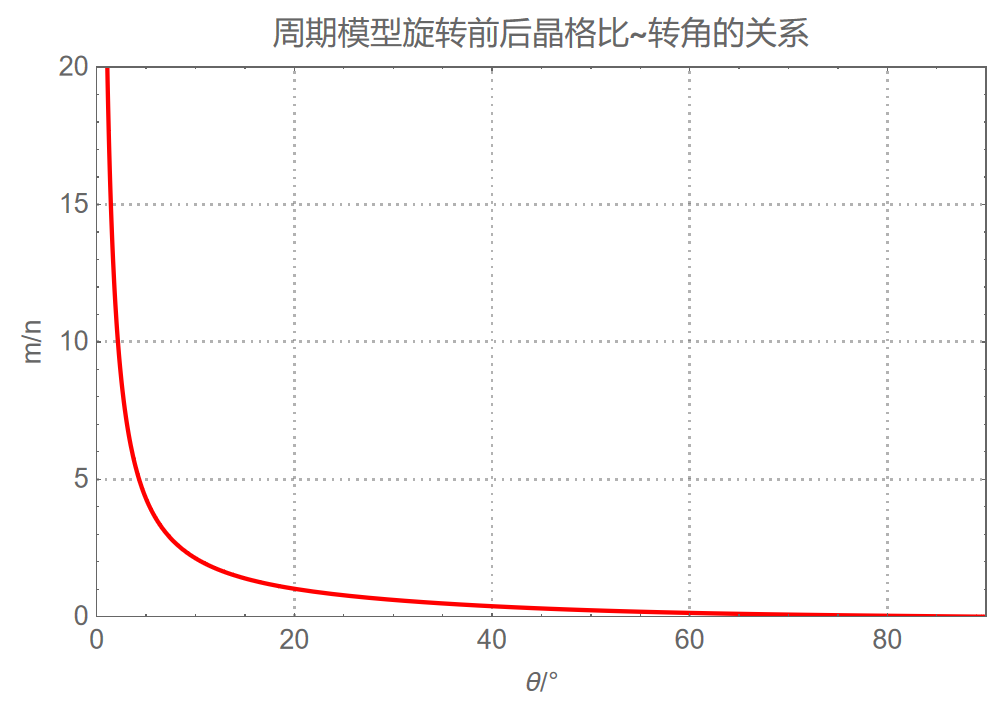
可以看出，要想将容差控制在大约10%以内，取向角被限制在0~20度。

范例

S2层粗粒化模型元胞满足，对于不同的取向角可以取不同的值。

n m p
10 21 2.1248 10 87.5187 496.343
1 1 1.0164 20 8.20848 22.5526
16 10 0.611312 30 120 207.846
21 10 0.483251 35 137.658 196.596

旋转周期性模型需要用倾斜的盒子！

本文采用CC-BY-SA-3.0协议，转载请注明出处
作者: 得意喵~