n维球以及n维正n+1面体的体积与表面积 · 得意喵~

n维球以及n维正n+1面体的体积与表面积

一个递归方法的应用:

求 $\int x^m e^xdx$

$\int{x^m *e^xdx}=x^m e^x-m\int x^{m-1} e^xdx$

递归表达式为: $F_m=x^m e^x-mF_{m-1}$

1 2	Simplify@RSolve[{f[n] == x^nExp[x] - nf[n - 1], f[1] == (x - 1) Exp[x]}, f[n], n] // TraditionalForm

$F_n= (-1)^{n+1} (-x)^{-n} \left((-1)^{n+1} x^n \text{Gamma2}(n+1,-x) +\Gamma (n+1) \left((-x)^n \text{Gamma2}(2,-x)\\+(-1)^n x^n+ (x-1) e^x (-x)^n-(-x)^n\right)\right)$

对球和正n+1面体:

1 球:

$V_n(r)=\int_{-r}^{r} V_{n-1}(\sqrt{r^2-y^2})dy$

换元后

$A_n=A_{n-1}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}cos^n\theta d\theta$

Clear["`*"];
g[n] = Integrate[Cos[x]^n, {x, -Pi/2, Pi/2}, Assumptions -> n > 0];
RSolve[{a[n] == a[n - 1]*g[n], a[1] == 2}, a[n], n] // 
  TraditionalForm ;
f[n_] := (2 \[Pi]^(n/2))/(n Gamma[n/2]);
ListPlot[Table[(2 \[Pi]^(n/2))/(n Gamma[n/2]), {n, 0, 20}]];
ListPlot[Table[f[x], {x, 0, 20, 0.02}], PlotTheme -> "Detailed"]
Max[Table[f[x], {x, 5, 6, 0.0001}]];

ListPlot[Table[(f[x + 0.0001] - f[x])/0.0001, {x, 5, 6, 0.0001}]];
FindRoot[D[f[x], x], {x, 1, 10}];
L[n_] = Simplify[n*f[n]];
ListPlot[Table[L[n], {n, 0, 20, 0.02}], PlotTheme -> "Detailed"];
FindRoot[D[L[x], x], {x, 1, 10}];
Integrate[f[2*x], {x, 0, Infinity}, 
 Assumptions -> x \[Element] Integer]
Sum[f[x], {x, 0, Infinity}]
Sum[L[2*n + 1], {n, 0, Infinity}]

体积系数:

$\frac{2 \pi ^{n/2}}{n \Gamma \left(\frac{n}{2}\right)}$

表面积系数:

$L_n=\frac{2 \pi ^{n/2}}{\Gamma \left(\frac{n}{2}\right)}$

绘图:

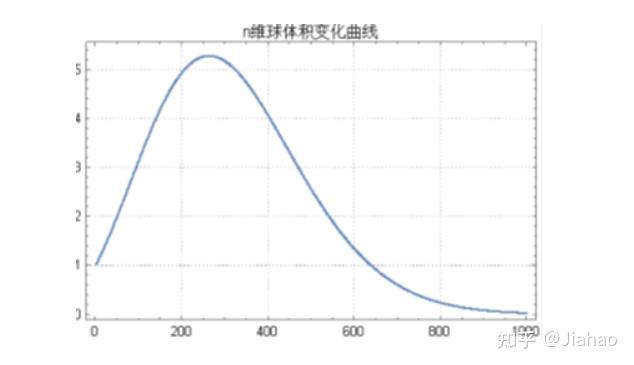
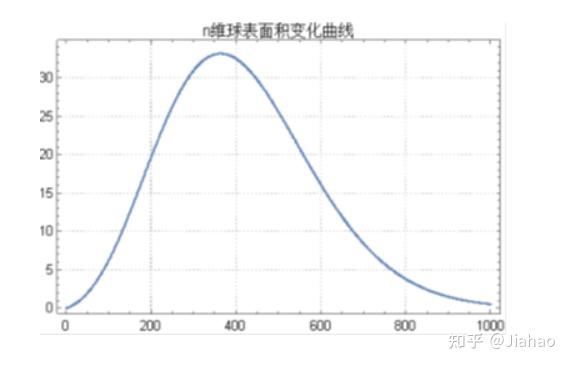
n维球在n=5.257是体积系数有最大值,5.27777

在n=7.257时表面积系数有最大值,33.1612

为啥呢?

我也不知道了.

体积系数和表面积系数是收敛的:

求和有:

体积系数和： $e^{\pi } \text{erf}\left(\sqrt{\pi }\right)+e^{\pi }$

$erf(x)$ 为误差函数。 $\text{erf}(z)=\frac{2}{\sqrt{\pi }}\int _0^zd t e^{-t^2}$

偶数项和: $e^{\pi }$

奇数项和： $e^{\pi } \text{erf}\left(\sqrt{\pi }\right)$

表面积系数和： $2 \left(e^{\pi } \pi \text{erf}\left(\sqrt{\pi }\right)+e^{\pi } \pi +1\right)$

偶数项和： $2 e^{\pi } \pi$

奇数项和： $2 \left(e^{\pi } \pi \text{erf}\left(\sqrt{\pi }\right)+1\right)$

2 正n+1面体:

高系数递推公式:

$H_n=\sqrt{1-(\frac{n-1}{n}H_{n-1})^2}$

1	H_n=\sqrt{1-(\frac{n-1}{n}H_{n-1})^2}

体积系数的递推公式：

$A_n=\frac{1}{n}A_{n-1}H_n$

1 2	a[n_] := -((I^n Sqrt[(-1)^n (n + n^2)])/(Sqrt[2] n)); RSolve[{b[n] == 1/na[n]b[n - 1], b[2] == Sqrt[3]/4}, b[n], n];

高系数：

$H_n=-\frac{i^n \sqrt{(-1)^n \left(n^2+n\right)}}{\sqrt{2} n}$

体积系数:

$A_n=\frac{(-1)^{\frac{1}{4} n (n+1)} (-i)^{2 n} 2^{\frac{1}{2}-\frac{n}{2}} \sqrt{i^{n (n+1)} (2)_{n-1} (3)_{n-1}}}{\left((1)_n\right){}^2}$

表面积系数:

$L_n=\frac{(-1)^{\frac{1}{4} n (n+1)} (-i)^{2 n} 2^{\frac{1}{2}-\frac{n}{2}} \sqrt{i^{n (n+1)} (2)_{n-1} (3)_{n-1}}}{\left((1)_n\right){}^2}$

为什么会有复数?

不知道了.可以画幅频曲线，相频曲线？？

注：以前看过网上有一个日本高考题，证明 $e^\pi>21$ ，使用的线性化方法。

可以出一个题：证明偶数维球体积系数之和大于21.

本文采用CC-BY-SA-3.0协议，转载请注明出处
作者: 得意喵~